Arc Length Calculator

Arc length calculator

Our arc length calculator can be used to measure the length of an arc and the sector area of a circle by using the measurements of the radius of a circle and the angle forming between both points of an arc. It can calculate sector area of a circle, arc length, length of a chord in a circle, and diameter of the circle at the same time. It provides the calculation in radian as well as in degree. Whether you need your calculations in degrees or radian, you don’t have to convert the answers because it calculates both types of angles for you. It is also called the curve length calculator.

Radian is a standard unit for the measurement of angular shapes. It is a system international derived unit and widely used in several areas of mathematics. One radian is equal to 57.29 degrees. Radian has a standard symbol rad to represent it. To convert radian into degree, use 1rad = 180/ π.

Degree is also used to measure the angles in mathematics, but it is not a system international unit for measuring the angular shapes. It has been used in the past.

It is denoted by the symbol “°”.

1 degree is equal to π/180 radians.

What is an Arc?

An arc is a segment or a section of the curve. It is represented by the symbol “⌒.”  The term arc is mostly used in geometry in circular shapes.

What is arc length?

Arc length is defined as the total distance between the two points of a section of a curved shape or a circle. If the shape is irregular, it will be called rectification of a curve instead of arc length. The circumference of a circle can also be used as the full arc length of that circle.

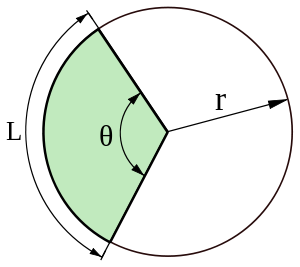
Arc length formula

The arc's length relies on the central angle θ and the circle's radius. The length of minor arc calculator is equal to the circumference of the circle if the angle is 360 degrees or 2π. The ratio of angle to arc length is therefore constant, that’s why:

L / θ = C / 2π

By substituting the circumference of a circle (C = 2πr) in the above equation, 

L / θ = 2πr / 2π

After simplifying the equation, we get:

L / θ = r

Multiply with θ on both sides of the equation to get the formula for arc length.

 L = r * θ

If we describe arc formula in words, it is the length that is equal to the central angle multiplied by the radius of a circle.

How to find the Arc length?

The arc length of a circle can be found by using two different methods. There are two scenarios to calculate the length of a curve. It depends on the unit of the angle. It could be in radian or degree. For either of them, different arc length equations are used to calculate the length of an arc.

• If the central angle is measured in radians

If the central angle is measured in radians, then the formula derived above will be used to find the arc length. 

L = r * θ

In this equation, r is the radius of the circle, and θ is the central angle of the arc measured in radians. 

Now let's suppose we have a circle with a radius of 12cm, and the angle forming between the two points of the circle is 4.22 radian. Put both of the values in the equation.

L = 12 * 4.22

By multiplying both, we get:

L = 50.64cm

The length of an arc with a central angle of 4.22 radians and a radius of 12 cm will be equal to 50.64cm.

It is important to have the measurement of the central angle in radians for this method. If you have the central angle in degrees, it is not valid for this method, and the arc length will not be correct. Radians and degrees can be converted to each other, as stated above, with formulas to convert.

• If the central angle is measured in degrees

There is a different formula for calculating the arc length if the central angle is measured in degrees. The length of the curve can be calculated by using this formula if the central angle is in degrees.

L = 2 πr (θ/360)

θ is the measure of the central angle of the arc in degrees, and r is the radius of the circle in this equation.

Suppose the central angle of the arc is 271.78 degrees, and the radius of the circle is 12cm, as in the above example. Put these values in the above equation to get the arc’s length.

L = 2π * 12 (271.78/360)

Since π = 3.14, substitute the value of π in the equation

L = 2*3.14*12 (271.78/360)

First, divide the central angle with 360 and then multiply the radius with two and value of π.

L = 75.36 (0.7549)

L = 56.89cm

So, the arc length of a circle with a radius of 12cm and the central angle of the arc of 271.78 degrees will be 56.89cm. Both methods are different because different units are used to measure of minor arc calculator and the central angle of the arc. Radian is most widely used, though, and is included in the standard system international unit. The degree is not used that widely, but still, you should know the method to calculate the arc’s length if the central angle is provided in degrees as in many math problems.

Area of a circular sector

The area of a sector of a circle is also called a circular sector. It is the part of a disk having an arc and two radii in which the larger region is regarded as the major sector and the smaller as the minor sector.

Area of circular sector Formula

We will first derive the formula for the area of the circular sector from the formula for the area of a circle. As we know the formula for the area of a circle is:

A = πr2

The sector area of a circle can be determined by multiplying the area of the circle by 2π and the ratio of angle.

A / θ = πr² / 2π

A / θ = r² / 2

SO, the final equation for the area of a sector of a circle is:

A = r² * θ / 2

Now suppose, we have a circle with a radius of 4cm and 45-degree angle. Put these values in the above equation.

A = 42 * 45/2

A = 16 * 22.5

A = 360cm

So, the area of the sector of circle will be 360cm with 4cm radius and angle of 45 degrees.

How to find chord length?

A chord is a line section that links a circumference of a circle with two ends. The chord length of a circle can be calculated if the radius and the angle between two radius lines. It can also be calculated by using the length of the perpendicular line from the center of the circle to the chord.

Arc length calculator with steps also calculates the chord length with ease in a single step. It is also used as a chord length calculator. Let’s find out the formula for calculating the length of the chord.

Chord length Formula

Below is the formula for measuring the length of a chord in a circle.

c = 2r sin (θ/2)

In this equation, r is the radius of the circle, and θ is the angle developed between two radius lines.

Suppose we have a circle with a radius of 5cm, and the angle is 40 degrees between both radius lines. Put these values in the equation above to find the length of the chord in a circle.

c = 2 * 4 sin (40/2)

After simplifying the equation,

c = 8 sin (20)

c = 8 sin20

Since sin20 = 0.9129

c = 8 * 0.9129

c = 7.30cm

So, the chord length will be 7.30cm for a 4cm radius and 40-degree angle.