Calcular Promedio
Calcular Promedio
Nuestra calculadora promedio puede calcular el promedio de calificaciones para el conjunto de datos dado en muy poco tiempo. Solo tiene que insertar el valor en el cuadro de entrada dado y presionar el botón "Calcular". Proporcionará instantáneamente el valor promedio, el valor de suma y el recuento promedio (número total de artículos).
Esta calculadora de valor promedio en línea tiene dos pestañas. Hay una razón detrás de la vista de dos pestañas. Hay una razón detrás de la vista de dos pestañas. La primera pestaña se llama pestaña "Valor único". Tiene un único cuadro de entrada donde todos los valores se pueden ingresar separados por comas. Es necesario separar los valores por comas. De lo contrario, no le dará los mejores resultados. Por otro lado, si necesita ingresar un valor separado, entonces la pestaña “Entrada múltiple” cumplirá con sus requisitos.
La pestaña de entrada múltiple tiene seis cuadros de entrada por defecto, y se pueden agregar más cuadros de entrada haciendo clic en el botón "Agregar más campos". Los usuarios pueden agregar tantos cuadros de entrada como sea necesario para calcular el promedio de su conjunto de datos. Estos cuadros de entrada agregados también se pueden eliminar mediante el uso de un pequeño botón rojo contra cada cuadro de entrada. Nuestra herramienta de búsqueda promedio tiene la precisión y velocidad perfectas para cumplir con los requisitos del entorno de trabajo de ritmo rápido de hoy.
Como sacar promedio de calificaciones?
El promedio tiene varios significados en diferentes contextos. En matemáticas, es un valor central que representa un grupo de datos para comprender el valor general de los datos presentados. Se calcula sumando todos los valores de los datos dados y dividiendo el resultado de la suma por el número total de valores en el conjunto de datos. Vamos a entenderlo con un simple ejemplo.
Supongamos que un estudiante obtuvo 40 puntos en física, 50 en matemáticas, 55 en química y 60 en inglés. Todos los cursos consisten en 100 puntos por curso. ¿Cuáles serán las calificaciones promedio del estudiante?
como calcular el promedio?
Para calcular las calificaciones promedio del estudiante, primero, tenemos que agregar todas las calificaciones obtenidas.
40 + 50 + 55 + 60 = 205
El total de calificaciones obtenidas son 205, de 400. Hay un total de 4 cursos. Entonces, dividiremos 205 entre 4 para obtener las calificaciones promedio. Al dividir obtenemos:
205/4 = 51.25
Entonces, las calificaciones promedio del estudiante son 51.25. Podemos deducir que el alumno obtuvo 51.25 puntos por curso. El promedio nos dio una visión general del desempeño del estudiante.
Tipos de promedio
Hay tres tipos de promedio. Media, mediana y moda. Discutiremos brevemente los tipos de promedio para obtener una buena comprensión del promedio.
1. Media o media aritmética
La media, que también se conoce como la media aritmética, es el valor central, que se estima para evaluar el valor central de un conjunto de datos dado. Esta medida matemática es el promedio más utilizado y generalmente se llama media en la vida diaria.
La suma de todos los valores en un conjunto de datos se calcula para calcular la media aritmética. La suma de los valores luego se divide por el número total de valores en los datos.
La media aritmética se debe usar si un conjunto de datos incluye valores que no son extremadamente altos o bajos y están razonablemente distribuidos de manera equitativa.
La fórmula para la media
Aunque la fórmula matemática no es relevante para calcular la media, puede ser útil conocer la fórmula básica para calcular la media aritmética. La media aritmética se puede calcular utilizando la siguiente fórmula.
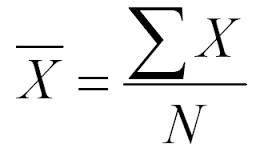
En esta ecuación de media aritmética, x̅ se refiere a la media aritmética y se lee como barra X. Σ se conoce como sigma, y es una palabra griega que representa el término "suma". La X representa cada valor individual en el conjunto de datos, y N es el número total de valores. Esta fórmula se puede describir como: la media aritmética es igual a la suma de cada valor dividido por el número total de participantes en el conjunto de datos.
2. Mediana
La mediana es otro tipo de promedio que se usa más comúnmente después de la media aritmética. Es el valor medio en un conjunto de datos ordenados. Los valores se ordenan en orden superior a inferior o en orden inferior a superior para calcular la mediana. La mediana varía según el número total de valores en el conjunto de datos.
Si el número total de valores en datos dados es par, por ejemplo, {2, 4, 6, 8 10}, calcularemos la mediana excluyendo un valor de cada lado del conjunto de datos. El valor restante será la mediana, que es 6 en este conjunto de datos.
Si el número total de valores es impar en un conjunto de datos, por ejemplo, {2, 4, 6, 8, 10, 12}, calcularemos la mediana de la misma manera, pero al final habrá dos valores. En este caso, esos dos valores son 6 y 8. Simplemente suma 6 y 8 y divide entre 2 para obtener la mediana. En este ejemplo, 7 es la mediana.
Fórmula mediana
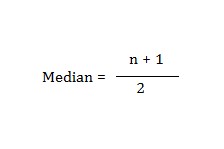
3. Modo
Por ejemplo, en el conjunto de datos {2, 4, 6, 7, 7, 8, 8, 0, 5}, 7 y 8 se repiten dos veces, lo que es más que cualquier otro valor. Por lo tanto, el modo en este conjunto de datos es 7 y 8. Este método puede usarse para calcular el modo en un conjunto de datos no agrupados. Para datos agrupados, se usa una fórmula para evaluar el modo.
Fórmula de modo
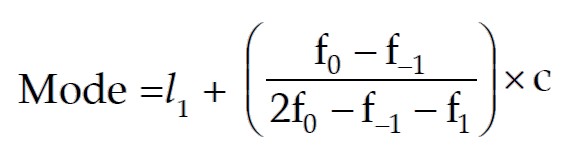
Aplicaciones de media
El promedio se usa en todos los ámbitos de la vida con frecuencia. Es utilizado por estudiantes, maestros, comerciantes, empresarios, ingenieros en su rutina diaria. No estaría mal que casi todas las personas usen el promedio en su vida en algún momento.
Es posible que escuche en un canal de noticias que las personas pasan un promedio de 12 horas de su tiempo por día en sus teléfonos móviles. No significa que cada persona pase 12 horas en el teléfono móvil.
Este promedio de calculadora de calificaciones se puede calcular en función de un conjunto de datos recopilados de áreas y personas específicas para tener una idea de cuántas horas pasan las personas en sus teléfonos. Algunos pueden usar su teléfono durante 4 horas, algunos durante seis o algunos durante 15 horas.
Los datos siempre varían al calcular el promedio, pero nos dan una visión general del uso de teléfonos móviles por parte de los usuarios. Este ejemplo es muy simple y, de la misma manera, el promedio se usa para resumir grandes números y datos en un solo número.